출처: https://school.programmers.co.kr/learn/courses/30/lessons/12979
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
N개의 아파트가 일렬로 쭉 늘어서 있습니다. 이 중에서 일부 아파트 옥상에는 4g 기지국이 설치되어 있습니다. 기술이 발전해 5g 수요가 높아져 4g 기지국을 5g 기지국으로 바꾸려 합니다. 그런데 5g 기지국은 4g 기지국보다 전달 범위가 좁아, 4g 기지국을 5g 기지국으로 바꾸면 어떤 아파트에는 전파가 도달하지 않습니다.
예를 들어 11개의 아파트가 쭉 늘어서 있고, [4, 11] 번째 아파트 옥상에는 4g 기지국이 설치되어 있습니다. 만약 이 4g 기지국이 전파 도달 거리가 1인 5g 기지국으로 바뀔 경우 모든 아파트에 전파를 전달할 수 없습니다. (전파의 도달 거리가 W일 땐, 기지국이 설치된 아파트를 기준으로 전파를 양쪽으로 W만큼 전달할 수 있습니다.)
- 초기에, 1, 2, 6, 7, 8, 9번째 아파트에는 전파가 전달되지 않습니다.
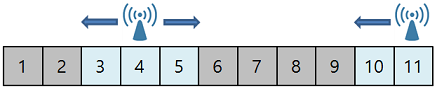
- 1, 7, 9번째 아파트 옥상에 기지국을 설치할 경우, 모든 아파트에 전파를 전달할 수 있습니다.
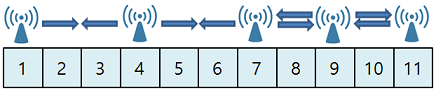
- 더 많은 아파트 옥상에 기지국을 설치하면 모든 아파트에 전파를 전달할 수 있습니다.
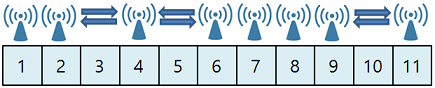
이때, 우리는 5g 기지국을 최소로 설치하면서 모든 아파트에 전파를 전달하려고 합니다. 위의 예시에선 최소 3개의 아파트 옥상에 기지국을 설치해야 모든 아파트에 전파를 전달할 수 있습니다.
아파트의 개수 N, 현재 기지국이 설치된 아파트의 번호가 담긴 1차원 배열 stations, 전파의 도달 거리 W가 매개변수로 주어질 때, 모든 아파트에 전파를 전달하기 위해 증설해야 할 기지국 개수의 최솟값을 리턴하는 solution 함수를 완성해주세요.
제한사항
- N: 200,000,000 이하의 자연수
- stations의 크기: 10,000 이하의 자연수
- stations는 오름차순으로 정렬되어 있고, 배열에 담긴 수는 N보다 같거나 작은 자연수입니다.
- W: 10,000 이하의 자연수
입출력 예
| N | stations | W | answer |
| 11 | [4, 11] | 1 | 3 |
| 16 | [9] | 2 | 3 |
문제 풀이
처음 문제를 풀기위해서 생각했던 방법은 1부터 N까지, stations의 위치를 기준으로 W만큼 도달되는 전파를 boolean 배열 혹은 int 배열에 저장하고 도달되지 않는 전파 위치를 찾아서 W만큼 도달되는 전파로 바꾸는 과정을 반복하였다.
이 방법으로 정확성 테스트는 무사히 통과하였지만 효율성에서는 시간초과가 났다.

N은 200,000,000 이하의 자연수인데 도달되는 전파를 하나하나 설정한다면 당연히 효율적이지 않고 효율성 테스트를
통과하지 않는 것도 당연하다. 스스로 생각하기에는 어려움이 있어서 구글링(킹갓)를 통해 대략적인 방법만을 터득하고
직접 코딩을 하는 방식을 선택했다. 항상 깨닫는게 있다면 규칙을 발견하면 정말 쉽다.
기지국 설치를 위한 규칙은
최적의 위치에 기지국을 설치하기 위해서는 왼쪽으로 W만큼, 오른쪽으로 W만큼 전파를 도달시켜야한다.

예시 #1으로 설명하자면 첫 번째 기지국은 최적의 위치이다. 왜냐하면 위치 4를 기준으로 왼쪽으로 W만큼 오른쪽으로 W만큼 전파가 다른 기지국에 간섭받지않고 도달하고 있다. 그렇다면 최적의 위치의 범위는 어느 정도일까?
자신의 위치에 전파가 있는 것은 당연하고, 왼쪽으로 W 오른쪽으로 W만큼 닿는다면 ( W * 2 + 1)의 범위를 지니고 있다.
여기 (+1)은 자신의 위치이다. 어? 이거는 당연한 소리자나? 하지만 이 규칙을 이용한다면 문제가 풀린다!
만약 전파가 닿지 않는 길이가 10이라고하고 예시와 같이 W는1이라고 하자.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
우선 눈대중으로 기지국의 최적의 위치를 살펴보자. 위의 그림에서는 2, 5, 8이 된다. 그리고 최적의 위치는 아니지만 위치10에 하나를 설치해야 완성이 된다. 눈치가 빠르신분들은 아차 싶으실거고 저와 같은 분들은 그래서? 라는 반응이 나온다.

간단하게 수식으로 설명하자면 기지국의 개수는 4개이다.
그리고 1~10의 범위의 길이는 10이다. 여기서 최적의 범위 (W * 2 + 1)를 나누어준다면?
10 / ( 1 * 2 + 1) = 3 이 된다. 간단한 수식을 통해 최적의 기지국 개수를 구했다.
그리고 최적의 기지국 개수로 나눈값을 뒤로하고 나머지가 존재한다면? 바로 위치 10이다.
이를 수식으로 한다면 if ( 10 % ( 1 * 2 + 1) != 0) 이다. 여기서 10 % ( 1* 2 + 1 ) = 1이다.
달리 말하면, ( 1 * 2 + 1 )이 3개있고 10 % ( 1 * 2 + 1 )이 0이 아니라면 1개가 있다라고 생각할 수 있다.
이제 범위에 따른 기지국 개수를 셀 수 있으니 세기만 하면 된다!
| class Solution { public int solution(int n, int[] stations, int w) { int answer = 0; int left = 1; //시작점 for (int A : stations) { int count = 0; if (A - left >= w + 1) { //시작점과 stations의 간격이 전파가 닿는지 안닿는지 체크 count += (A - left - w) / (w * 2 + 1); if ((A - left - w) % (w * 2 + 1) != 0) count++; } answer += count; left = A + w + 1; } if (left <= n) { // stations마지막에서 n 까지 전파가 닿는지 안닿는지 체크 int count = 0; count += (n - stations[stations.length - 1] - w) / (w * 2 + 1); if ((n - stations[stations.length - 1] - w) % (w * 2 + 1) != 0) count++; answer += count; } return answer; } } |
여기서 left 가 1로 시작하는데 1~N까지 세기 위해서 1로 시작하는 것이다.
그리고 반복문은 stations[0] 부터 시작하는데 left = 1부터 stations[0]까지 라고 생각하면 된다.
1부터 stations[0] 까지 기지국 개수를 구했다면 stations[0]에서 오른쪽으로 (w+1)을 left로 설정해야한다.
그리고 left부터 stations[1] 까지 기지국 개수를 구하는 것을 stations 마지막 까지 반복한다.
이렇게 구한다면 1~stations마지막까지 구할 수 있고 이제 stations마지막부터 n까지 구하는 것으로 마무리하면 된다.

끝!
'프로그래머스' 카테고리의 다른 글
| [프로그래머스/JAVA] 스티커모으기(2) (0) | 2022.12.09 |
|---|---|
| [프로그래머스/JAVA] 징검다리 건너기 (0) | 2022.12.06 |
| [프로그래머스/JAVA] 보석 쇼핑 (0) | 2022.12.01 |
| [프로그래머스/JAVA] 불량 사용자 (0) | 2022.11.29 |
| [프로그래머스/JAVA] 최고의 집합 (0) | 2022.11.22 |



